Prepare your own two magic squares of 5 rows and 5 columns in which the first row is of your choice. You can enter any 5 numbers between -9999 to 9999 (actually you can enter any number, but for the betterment of the look of the sheet, this restriction is implemented in the software) of your choice in the first row. The software will give you two different magic squares with your chosen numbers in 1 st row. These two magic squares have 120 types of the same addition.
Rows
|
5
|
Columns
|
5
|
Diagonals
|
2
|
Broken Diagonals
|
8
|
Different Patterns
|
100
|
Total
|
120
|
Click the following button for the software of magic squares of order 5 x 5.
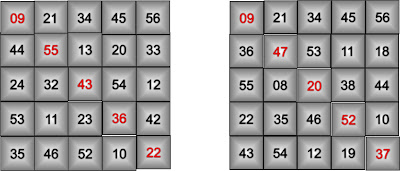
Now we will see all the properties of 5 x 5 magic squares one by one. Let us see the magic squares in which we choose the first row with the numbers 9, 21, 34, 45, and 56. The following two magic squares will be obtained by the software.
Now we will see all types of addition:
1) Addition of all the numbers in the Rows: (1 to 5)
a) First Row: (1/5)
09 + 21 + 34 + 45 + 56 = 165 09 + 21 + 34 + 45 + 56 = 165
b) Second Row: (2/5)
44 + 55 + 13 + 20 + 33 = 165 36 + 47 + 53 + 11 + 18 = 165
c) Third Row: (3/5)
24+ 32 + 43 + 54 + 54 = 165 55 + 47 + 20 + 38 + 44 = 165
d) Forth Row: (4/5)
55+ 11 + 23 + 36 + 42 = 165 22 + 35 + 46 + 52 + 10 = 165
35+ 46 + 52 + 10 + 22 = 165 43 + 54 + 12 + 19 + 37 = 165
2) Addition of all the numbers in the Columns: (6 to 10)
a) First Column: (6/10)
09+ 44 + 24 + 53 + 35 = 165 09 + 36 + 55 + 22 + 43 = 165
21+ 55 + 32 + 11 + 46 = 165 21 + 47 + 08 + 35 + 54 = 165
c) Third Column: (8/10)
34+ 13 + 43 + 23 + 52 = 165 34 + 53 + 20 + 46 + 12 = 165
d) Forth Column: (9/10)
45 + 20 + 54 + 36 + 10 = 165 45 + 11 + 38 + 52 + 19 = 165
e) Fifth Column: (10/10)
56 + 33 + 12 + 42 + 22 = 165 56 + 18 + 44 + 10 + 37 = 165
3) Addition of all the numbers in the Diagonals: (11 to 12)
a) First Diagonal: (11/12)
09 + 55 + 43 + 36 + 22 = 165 09 + 47 + 20 + 52 + 37 = 165
b) Second Diagonal: (12/12)
56 + 20 + 43 + 11 + 35 = 165 56 + 11 + 20 + 35 + 43 = 165
8 types of broken diagonal addition and 100 types of different patterns of addition will be published in the next blog.