136-Number pattern and its beauty

Nowadays, the following pattern is being observed on some social networks.

Nowadays, the next convention is being observed on some social networks.

Now we will see the basics behind this pattern of numbers.

For any positive integer "a" 

(100a+10a+a)/(a+a+a) = 111a/3a ---------- equation-1

                                     = 111/3               

                                     = 37. 

It's always 37 for such types of patterns of the problem.

Putting a = 1, in equation-1, we get 111/3 = 37.

Similarly, putting a = 2, we get 222/6 = 37, and so on.

These are simply the basics and everyone knows these basics of numbers. Now we will see some different patterns of numbers.

2 digits form:

If we take the same pattern for 2 digits, it will look like the following figure.

For any positive integer "a" 

(10a+a)/(a+a) = 11a/2a ---------- equation-2

                       = 11/2               

                       = 5.5. 

It's always 5.5 for such types of patterns of the problem.

Putting a = 1, in equation-2, we get 11/2 = 5.5.

Similarly, putting a = 2, we get 22/4 = 5.5, and so on.

4 digits form:

For any positive integer "a" 

(1000a+100a+10a+a)/(a+a+a+a) = 1111a/4a ---------- equation-3

                       = 1111/4               

                       = 277.75. 

It's always 277.75 for such types of patterns of the problem.

Putting a = 1, in equation-3, we get 1111/4 = 277.75.

Similarly, putting a = 2, we get 2222/8 = 277.75, and so on.

Note: The same explanation is there for all the following figures.

5 digits form:

6 digits form:

7 digits form:

8 digits form:

9 digits form:

The same concept can be applied to any number of digits. This is only the beauty of numbers.

There is nothing new. It is a well-known fact and the basics of numbers.

ANIL SATPUTE

135-Magic cube part-6

Click here for the previous blog on magic cube.

We have already seen the preparation of the magic cube.

Today we will discuss some specific addition patterns of this magic cube. See the following figure of the magic cube.

Here see all the boxes with all corresponding numbers. Now we study "Top-Bottom-Front-Left-Diagonal-strip". See the following diagram taken from the above magic cube.

Here the addition of all the corresponding numbers will be 1164.

ANIL SATPUTE

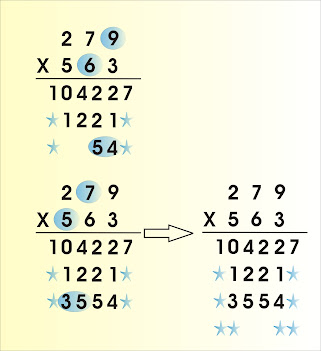
134-Important video on Simple method of multiplication

 Video on a simple method of multiplication.

For more details on multiplication, click on the following link:

Click here for the previous blog on a simple method of multiplication

Example: Multiply  279 by 563.

Step-1

Step-2

Step-3

Step-4

Click here to see the video on the fun with mathematics 

ANIL SATPUTE

133-Important video on fun with mathematics

Video on the fun with mathematics.

1) Basics of drawing perpendicular bisector on the line segment.

2) Funny addition.

3) Basics of roots of quadratic equations.

4) Practical way to prove, the sum of the angles of a triangle is 180 degrees.

5) Fun with  3², 33², 333^2, and so on.

6) Fun with 6², 66², 666^2, and so on.

7) Fun with 9², 99², 999^2, and so on.

8) Digit addition.

9) Check your calculations.

All such fun will be enjoyed in the following video. If you like this video, then subscribe to my channel and share and like this video.

Click here to see the video on the fun with mathematics 

ANIL SATPUTE

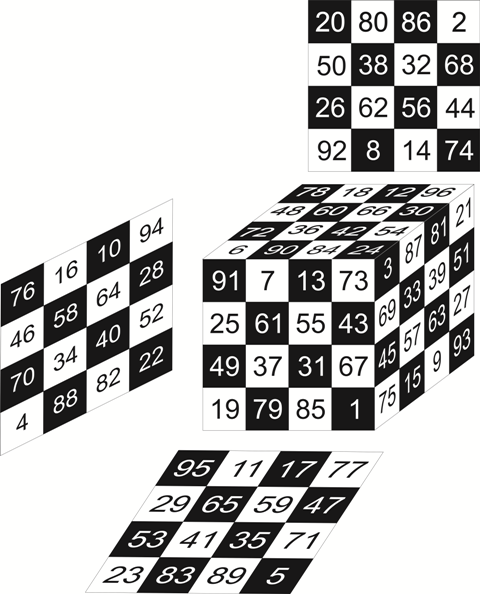
132-Magic cube part-5

Click here for the previous blog on magic cube.

We have already seen the preparation of the magic cube.

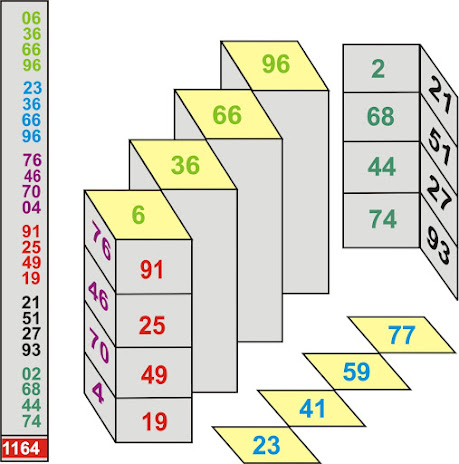
Today we will discuss some specific addition patterns of this magic cube. See the following figure of the magic cube.

Here see all the boxes with all corresponding numbers. Now we study "Top-bottom-diagonal-front-right-strip". See the following diagram taken from the above magic cube.

Here the addition of all the corresponding numbers will be 1164.

Click here for the next blog on magic cube.

ANIL SATPUTE

131-Miraculous Constant 8181

 Miraculous Constant 8181

This work is a special birthday gift to my sweetheart, my wife Jyoti Satpute

Click here for software of Miraculous constant 8181

The ‘Kaprekar constant’ (6174) is a constant with special properties. The ‘Miraculous Constant’ is based on the ‘Kaprekar Constant’ and exhibits some special properties in addition to the properties of the ‘Kaprekar Constant’.

For any four-digit number that is made up of at least one differing digit, rearrange the digits as follows:
1)    Place the largest digit at the 1000’s place and the smallest digit at the 100’s place.
Out of the remaining 2 digits:
2)      Place the largest digit at the 10’s place and the smallest digit at the unit place.
Let's refer to this rearranged number as a Zigzag number.
Example: Let’s say the input number is 8492. Let’s form the Zigzag number from this.
Solution:
1)    The highest digit of the given number 8492 is 9 and the smallest digit is 2. So, the 1000’s placed digit of the Zigzag number will be 9, and the 100’s placed digit will be 2.
2)    Now we need to place the digits 8 and 4 where 8 is the greater and 4 is the smaller digit, so 10’s placed digit will be 8 and the units digit will be 4.
3)    So, here the zigzag number of 8492 will be 9284.
4)    Its reverse number will be 4829.

 In general, if the number is 1000a + 100b + 10c + d in which, a > b > c > d, ∀ a, b, c, d ∈ W, a set of whole numbers, then the Zigzag number will be 1000a + 100d + 10b + c and its reverse number is 1000c + 100b + 10d + a. At least one digit out of a, b, c, or d must be different from others.
Now let us take the positive difference between the “Zigzag number” and the “reverse number”.
Repeat this process called iteration until you get 8181 (Miraculous constant).

Introduction

Kaprekar's constant is 6174. Our interest is to develop some other criteria to get the Miraculous Constant 8181. Let us take any 4-digit number with at least one different digit. We can take any number like 0001 which has 4 digits and one digit is different.

Method

Let us take any 4-digit number, 8492. Here, the largest digit is 9. So, the thousand-place digit will be 9. The smallest digit is 2, so the 100s place digit is 2. From 8492, digits 9 and 2 are being used, so the remaining digits are 8 and 4. To place a larger digit, 8 at the 10s place and 4 at the units place. So, our Zigzag number is 9284 and its reverse number is 4829 and we get a positive difference.

Figure-1

The number of iterations for 8492 to get the Miraculous Constant 8181 is 8.

Here in iteration 3, the number 8181 is obtained. Again, from 8181 to reach 8181 we have 5 iterations, and they are fixed.