01) The number of elements in a set:
The Number of distinct elements in a finite set A is denoted by n (A).
02) Some Important Results:
Cartesian Product of two sets: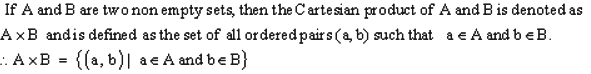
Relation:
If A and B are any two non-empty sets, then any subset of A x B is called a relation from A to B. If R is the relation from A to B and (x, y) belongs to R, then we say that xRy. Here Set A is the Domain and set B is the Co-Domain. Y is called the image of x under relation R. Similarly, x is called the pre-image of y under relation R.
Range:
A set of all the elements of Co-Domain B associated with the elements of Domain A is called the Range of Relation R.
Function:
A and B are two non-empty sets. The Function f from A to B is said to be a function if every element of set A is associated with the unique element of set B and is denoted as f: A -> B. and we say that y = f(x). Here y is the image of x under function f.
Here we say that A is the Domain and B is Co-Domain.
Range:
A set of all the elements of Co-Domain B associated with the elements of Domain A is called the Range of Function f.
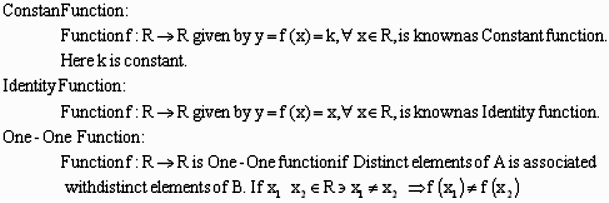
Onto Function:
f: A-> B is Onto function if every element of Co-Domain B is associated with some
elements of A under Function f. (Note: Range of function "f" is the same as Co-Domain).
Into Function:
f: A ->; B is Into function if there exists at least one element extra in Co-Domain B which is not associated with any element of Domain A under Function f. (Note: Range of function "f" is not same as Co-Domain).
Even Function:
f : A -> B is said to be Even Function if f (-x) = f (x).
Example: f (x) = cos x
Example: f (x) = x2
Odd Function:
f : A -> B is said to be Even Function if f (-x) = - f (x).
Example: f (x) = sin x
Example: f (x) = x3
If f: A ->; B, g : B-> C, then gof : A -> C where gof (x) = g[f(x)]
Inverse Function:
If f: A -> B is one-one onto Function, then g: B ->A is known as an inverse function of f and is denoted as f-1: B -> A.
The Number of distinct elements in a finite set A is denoted by n (A).
02) Some Important Results:
Cartesian Product of two sets:
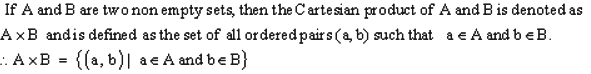
Relation:
If A and B are any two non-empty sets, then any subset of A x B is called a relation from A to B. If R is the relation from A to B and (x, y) belongs to R, then we say that xRy. Here Set A is the Domain and set B is the Co-Domain. Y is called the image of x under relation R. Similarly, x is called the pre-image of y under relation R.
Range:
A set of all the elements of Co-Domain B associated with the elements of Domain A is called the Range of Relation R.
Function:
A and B are two non-empty sets. The Function f from A to B is said to be a function if every element of set A is associated with the unique element of set B and is denoted as f: A -> B. and we say that y = f(x). Here y is the image of x under function f.
Here we say that A is the Domain and B is Co-Domain.
Range:
A set of all the elements of Co-Domain B associated with the elements of Domain A is called the Range of Function f.
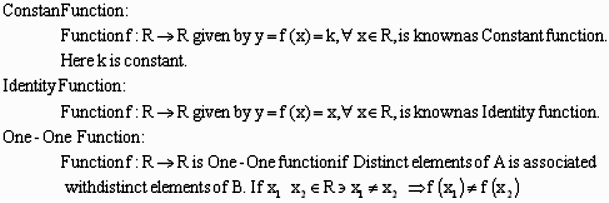
Onto Function:
f: A-> B is Onto function if every element of Co-Domain B is associated with some
elements of A under Function f. (Note: Range of function "f" is the same as Co-Domain).
Into Function:
f: A ->; B is Into function if there exists at least one element extra in Co-Domain B which is not associated with any element of Domain A under Function f. (Note: Range of function "f" is not same as Co-Domain).
Even Function:
f : A -> B is said to be Even Function if f (-x) = f (x).
Example: f (x) = cos x
Example: f (x) = x2
Odd Function:
f : A -> B is said to be Even Function if f (-x) = - f (x).
Example: f (x) = sin x
Example: f (x) = x3
Composite Function:
If f: A ->; B, g : B-> C, then gof : A -> C where gof (x) = g[f(x)]
Inverse Function:
If f: A -> B is one-one onto Function, then g: B ->A is known as an inverse function of f and is denoted as f-1: B -> A.









