NCERT10th MathematicsExercise 6.6Topic: 6 Triangles
Need help with math? We're here to help! Our resources include NCERT textbooks, lessons on Triangles, and more. Join our community of students and teachers today!
Need help with math? We're here to help! Our resources include NCERT textbooks, lessons on Triangles, and more. Join our community of students and teachers today!
Click here for ⇨ NCERT-10-6-Triangles - Ex- 6.5
EXERCISE 6.6
Q 1. In the following fig., PS is the bisector of ∠ QPR of ∆ PQR.
Prove that QS/SR = PQ/PR
Solution:1) Let us draw a line parallel to PS, through R, which intersects QP at T 2) So, PS || RT.3) As PS is the bisector of ∠ QPR,
∠ QPS = ∠ SPR ------- equation 1
4) As PS || RT,
∠ SPR = ∠ PRT (Alertnate angles) ------- equation 2
5) From equations 1 and 2 we have,
∠ QPS = ∠ PRT ------- equation 3
6) As PS || RT,
∠ QPS = ∠ PTR (Corresponding angles) ------- equation 4
7) From equations 3 and 4 we have,
∠ PRT = ∠ PTR ------- equation 5
8) From equation 5 we have,
(PR) = (PT) ------- equation 6
9) In ∆ QTR,
(QS)/(SR) = (QP)/(PT) (By BPT) ------- equation 7
10) From equations 5 and 6 we have,
(QS)/(SR) = (QP)/(PR), hence proved.
Q 2. In the following fig., D is a point on hypotenuse AC of ∆ ABC, such that
BD ⟂ AC, DM ⟂ BC, and DN ⟂ AB. Prove that :
(i) DM2 = DN . MC (ii) DN2 = DM . AN
a) ∠ DCM + ∠ CDM = 900 ------ equation 1(sum of the remaining angles of right-angled ∆)b) ∠ CDM + ∠ BDM = 900 (BD ⟂ AC) ------ equation 2
2) From equations 1 and 2 we have,
c) ∠ DCM + ∠ CDM = ∠ CDM + ∠ BDM
d) ∠ DCM = ∠ BDM ------ equation 3
3) In ∆ DMB,
3) In ∆ DMB,
a) ∠ DBM + ∠ BDM = 900 ------ equation 4
(sum of the remaining angles of right-angled ∆)
b) ∠ BDM + ∠ CDM = 900 (BD ⟂ AC, as given in equation 2) equation 5
4) From equations 4 and 5 we have,
c) ∠ DBM + ∠ BDM = ∠ BDM + ∠ CDM
d) ∠ DBM = ∠ CDM ------ equation 6
5) From equations 3 and 6 and by AA similarity test,
5) From equations 3 and 6 and by AA similarity test,
a) ∆ DBM ~ ∆ CDM --------- equation 7
6) As corresponding sides of similar triangles are proportional, we have,a) (DM)/(MC) = (BM)/(DM)
b) (DM) x (DM) = (BM) x (MC)
c) (DM)2 = (BM) x (MC)
7) As □ DNBM is a rectangle, BM = DN, so, we have,a) (DM)2 = (DN) x (MC), hence proved.
a) (DM)/(MC) = (BM)/(DM)
8) In ∆ AND,
8) In ∆ AND,
a) ∠ DAN + ∠ ADN = 900 ------ equation 8
(sum of the remaining angles of right-angled ∆)
b) ∠ ADN + ∠ BDN = 900 (BD ⟂ AC) ------ equation 9
b) ∠ ADN + ∠ BDN = 900 (BD ⟂ AC) ------ equation 9
9) From equations 8 and 9 we have,
c) ∠ DAN + ∠ ADN = ∠ ADN + ∠ BDN
c) ∠ DAN + ∠ ADN = ∠ ADN + ∠ BDN
d) ∠ DAN = ∠ BDN ------ equation 10
10) In ∆ DNB,
10) In ∆ DNB,
a) ∠ DBN + ∠ BDN = 900 ------ equation 11
(sum of the remaining angles of right-angled ∆)
b) ∠ BDN + ∠ ADN = 900 (BD ⟂ AC, as given in equation 9) equation 12
b) ∠ BDN + ∠ ADN = 900 (BD ⟂ AC, as given in equation 9) equation 12
11) From equations 11 and 12 we have,
c) ∠ DBN + ∠ BDN = ∠ BDN + ∠ ADN
c) ∠ DBN + ∠ BDN = ∠ BDN + ∠ ADN
d) ∠ DBN = ∠ ADN ------ equation 13
12) From equations 10 and 13 and by AA similarity test,
12) From equations 10 and 13 and by AA similarity test,
a) ∆ DBN ~ ∆ ADN --------- equation 14
13) As corresponding sides of similar triangles are proportional, we have,a) (DN)/(AN) = (BN)/(DN)
b) (DN) x (DN) = (BN) x (AN)
c) (DN)2 = (BN) x (AN)
14) As □ DNBM is a rectangle, BN = DM, so, we have,a) (DN)2 = (DM) x (AN), hence proved.
Q 3. In the following fig., ABC is a triangle in which ∠ ABC > 90° and AD ⟂ CB
a) (DN)/(AN) = (BN)/(DN)
produced. Prove that AC2 = AB2 + BC2 + 2 BC . BD.
Solution:
1) In ∆ ADB, by the theorem of Pythagoras, we have,(AB)2 = (AD)2 + (DB)2 ------- equation 1.
2) In ∆ ADC, by the theorem of Pythagoras, we have,(AC)2 = (AD)2 + (DC)2
1) In ∆ ADB, by the theorem of Pythagoras, we have,
(AB)2 = (AD)2 + (DB)2 ------- equation 1.
2) In ∆ ADC, by the theorem of Pythagoras, we have,
(AC)2 = (AD)2 + (DC)2
(AC)2 = (AD)2 + (DB + BC)2
(AC)2 = (AD)2 + (DB)2 + (BC)2 + 2 . DB . BC ------- equation 2.
3) From equations 1 and 2, we have,
(AC)2 = [(AD)2 + (DB)2] + (BC)2 + 2 . DB . BC
(AC)2 = (AB)2 + (BC)2 + 2 . BC . BD, hence proved.
Q 4. In the following fig., ABC is a triangle in which ∠ABC < 90° and AD ⟂ BC.
Prove that AC2 = AB2 + BC2 – 2 BC . BD.
Solution: 1) In ∆ ADB, by the theorem of Pythagoras, we have,(AB)2 = (AD)2 + (BD)2 ------- equation 1.
2) In ∆ ADC, by the theorem of Pythagoras, we have,(AC)2 = (AD)2 + (DC)2
1) In ∆ ADB, by the theorem of Pythagoras, we have,
(AB)2 = (AD)2 + (BD)2 ------- equation 1.
2) In ∆ ADC, by the theorem of Pythagoras, we have,
(AC)2 = (AD)2 + (DC)2
(AC)2 = (AD)2 + (BC - BD)2
(AC)2 = (AD)2 + (BC)2 + (BD)2 - 2 . BC . BD ------- equation 2.
3) From equations 1 and 2, we have,
(AC)2 = (AD)2 + (BD)2 + (BC)2 - 2 . BC . BD
(AC)2 = [(AD)2 + (BD)2]+ (BC)2 - 2 . BC . BD
(AC)2 = [(AB)2]+ (BC)2 - 2 . BC . BD
(AC)2 = (AB)2+ (BC)2 - 2 . BC . BD, hence proved.
Q 5. In the following fig., AD is a median of a triangle ABC and AM ⟂ BC.
Prove that :
(i) AC2 = AD2 + BC . DM + (BC/2)2(ii) AB2 = AD2 - BC . DM + (BC/2)2(iii) (AC)2 + (AB)2 = 2 (AD)2 + (1/2)(BC)2
Solution:(i) AC2 = AD2 + BC . DM + (BC/2)2
1) In ∆ AMD, by the theorem of Pythagoras, we get,(AD)2 = (AM)2 + (MD)2 ------- equation 1.
2) In ∆ AMC, by the theorem of Pythagoras, we get,(AC)2 = (AM)2 + (MC)2
(AC)2 = (AM)2 + (MD + DC)2
(AC)2 = (AM)2 + (MD)2 + (DC)2 + 2 (MD) (DC) ------- equation 2.
3) From equations 1 and 2, we have,
(AC)2 = (AM)2 + (MD)2 + (DC)2 + 2 (MD) (DC)
(AC)2 = [(AD)2] + (DC)2 + 2 (MD) (DC) ------- equation 3.
4) As (DC) = (1/2) (BC), so from equation 3 we have
(AC)2 = [(AD)2] + (BC/2)2 + 2 (MD) (DC)
(AC)2 = [(AD)2] + (BC/2)2 + [2 (DC)] (MD) [since 2 (DC) = (BC)],
(AC)2 = [(AD)2] + (BC/2)2 + (BC) (MD)(AC)2 = (AD)2 + (BC) (DM) + (BC/2)2 ------- equation 4.
5) (AC)2 = (AD)2 + (BC) (DM) + (BC/2)2, hence proved.
(ii) AB2 = AD2 - BC . DM + (BC/2)2
6) In ∆ AMB, by the theorem of Pythagoras, we get,(AB)2 = (AM)2 + (BM)2
(AB)2 = (AM)2 + (BD - DM)2
(AB)2 = (AM)2 + (BD)2 + (DM)2 - 2 (BD) (DM)
(AB)2 = [(AM)2 + (DM)2] + (BD)2 - 2 (BD) (DM)
(AB)2 = [(AD)2] + (BC/2)2 - 2 (BC/2) (DM)(AB)2 = (AD)2 + (BC/2)2 - (BC) (DM) ------- equation 5.
7) (AB)2 = (AD)2 + (BC/2)2 - (BC) (DM), hence proved
(iii) (AC)2 + (AB)2 = 2 (AD)2 + (1/2)(BC)2
8) Adding equations 4 and 5, we get,(AC)2 + (AB)2 = (AD)2 + (BC) (DM) + (BC/2)2 + (AD)2 + (BC/2)2 - (BC) (DM)
(AC)2 + (AB)2 = 2 (AD)2 + 2 (BC/2)2
(AC)2 + (AB)2 = 2 (AD)2 + 2 (BC)2/4
(AC)2 + (AB)2 = 2 (AD)2 + 1/2 (BC)2
9) (AC)2 + (AB)2 = 2 (AD)2 + 1/2 (BC)2, hence proved.
Q 6. Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
Solution:
1) In ∆ ACF, by the theorem of Pythagoras, we get,(AC)2 = (AF)2 + (CF)2 ------- equation 1.
2) In ∆ AFD, by the theorem of Pythagoras, we get,(AF)2 = (AD)2 - (DF)2 ------- equation 2.
3) According to the diagram, we have,
(CF) = (DC - DF) ------- equation 3.
4) From equations 1, 2, and 3, we have,
(AC)2 = (AF)2 + (CF)2
(AC)2 = [(AD)2 - (DF)2] + (DC - DF)2
(AC)2 = (AD)2 - (DF)2 + (DC)2 + (DF)2 - 2 (DC) (DF)
(AC)2 = (AD)2 + (DC)2 - 2 (DC) (DF) ------- equation 4.
5) In ∆ BDE, by the theorem of Pythagoras, we get,(BD)2 = (ED)2 + (BE)2 ------- equation 5.
6) In ∆ DEA, by the theorem of Pythagoras, we get,(ED)2 = (AD)2 - (AE)2 ------- equation 6.
7) According to the diagram, we have,
(BE) = (BA + AE) ------- equation 7.
8) From equations 5, 6, and 7, we have,
(BD)2 = (ED)2 + (BE)2
(BD)2 = [(AD)2 - (AE)2] + (BA + AE)2
(BD)2 = (AD)2 - (AE)2 + (BA)2 + (AE)2 + 2 (BA) (AE)
(BD)2 = (AD)2 + (BA)2 + 2 (BA) (AE) ------- equation 8.
9) Adding equations 4 and 8, we get,(AC)2 + (BD)2 = [(AD)2 + (DC)2 - 2 (DC) (DF)] + [(AD)2 + (BA)2 + 2 (BA) (AE)]
------- equation 9.
10) According to the diagram, we know that,
a) (AD) = (BC)
b) (BA) = (DC)11) So, we will change the red-colored terms of equation 9 as follows:
a) (AE) = (DF)
(AC)2 + (BD)2 = [(AD)2 + (DC)2 - 2 (DC) (DF)] + [(AD)2 + (BA)2 + 2 (BA) (AE)]
(AC)2 + (BD)2 = [(AD)2 + (DC)2 - 2 (DC) (DF)] + [(BC)2 + (BA)2 + 2 (DC) (DF)]
(AC)2 + (BD)2 = [(AD)2 + (DC)2] + [(BC)2 + (BA)2] ------- equation 10.
12) From equation 10, we can say that,
The sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides.
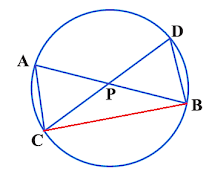
Q 7. In the following fig., two chords AB and CD intersect each other
at point P. Prove that :
(i) ∆ APC ~ ∆ DPB (ii) AP . PB = CP . DP
Solution:(i) ∆ APC ~ ∆ DPB
1) In ∆ APC and ∆ DPB,a) < APC = < DPB (vertically opposite angles are equal)
b) < CAP = < BDP (angles inscribed in the same arc are equal)2) So, by AA similarity test, ∆ APC ~ ∆ DPB, hence proved.
(ii) AP . PB = CP . DP
1) We proved that,
(i) ∆ APC ~ ∆ DPB
1) In ∆ APC and ∆ DPB,
a) < APC = < DPB (vertically opposite angles are equal)
b) < CAP = < BDP (angles inscribed in the same arc are equal)
2) So, by AA similarity test, ∆ APC ~ ∆ DPB, hence proved.
(ii) AP . PB = CP . DP
1) We proved that,
∆ APC ~ ∆ DPB
2) So, as corresponding sides are proportional, we have,(AP)/(DP) = (CP)/(PB)
2) So, as corresponding sides are proportional, we have,
(AP)/(DP) = (CP)/(PB)
(AP) . (PB) = (CP) . (DP), hence proved.
Q 8. In the following fig., two chords AB and CD of a circle intersect each
other at the point P (when produced) outside the circle. Prove that
(i) ∆ PAC ~ ∆ PDB (ii) PA . PB = PC . PD
Solution:
(i) ∆ PAC ~ ∆ PDB
1) In ∆ PAC and ∆ PDB,a) < APC = < DPB (common angles)
b) < CAP = < BDP (Exterior angle of a cyclic quadrilateral is equal to the
(i) ∆ PAC ~ ∆ PDB
1) In ∆ PAC and ∆ PDB,
a) < APC = < DPB (common angles)
b) < CAP = < BDP (Exterior angle of a cyclic quadrilateral is equal to the
opposite interior)
2) So, by AA similarity test, ∆ PAC ~ ∆ PDB, hence proved.
(ii) PA . PB = PC . PD
1) We proved that,
2) So, by AA similarity test, ∆ PAC ~ ∆ PDB, hence proved.
(ii) PA . PB = PC . PD
1) We proved that,
∆ PAC ~ ∆ PDB
2) So, as corresponding sides are proportional, we have,(PA)/(PD) = (PC)/(PB)
2) So, as corresponding sides are proportional, we have,
(PA)/(PD) = (PC)/(PB)
(PA) . (PB) = (PC) . (PD), hence proved.
Q 9. In the following fig., D is a point on side BC of ∆ ABC
such that BD/CD = AB/AC
Prove that AD is the bisector of ∠ BAC.
Solution:1) It is given that,
a) (BD)/(CD) = (BA)/(AC)
2) So, using the converse of the basic proportionality theorem,
a) AD || EC
b) ∠ BAD = ∠ AEC (corresponding angles) ------ equation 1
c) ∠ CAD = ∠ ACE (alternet interior angles) ------ equation 2
3) As (AE) = (AC),
a) ∠ AEC = ∠ ACE ------ equation 3
4) From equations 1 and 3, we get,
a) ∠ BAD = ∠ ACE ------ equation 4
5) From equations 2 and 4, we get,
a) ∠ BAD = ∠ CAD ------ equation 5
6) From equation 5, we get,
a) AD is the bisector of ∠ BAC, hence proved.
Q 10. Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see the following fig.)? If she pulls in the string at
the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
(Note: See the original figure in the text-book)
Solution:
1) Let AB be the distance between the tip of the fishing rod and the water surface.2) Let BC be the distance between the fly and the rod.3) In ∆ ABC, by the theorem of Pythagoras, we get,
(AC)2 = (AB)2 + (BC)2
(AC)2 = (1.8)2 + (2.4)2
(AC)2 = (3 x 0.6)2 + (3 x 0.8)2
(AC)2 = [(3)2 x (0.6)2] + [(3)2 x (0.8)2]
(AC)2 = (3)2 x [(0.6)2 + (0.8)2]
(AC)2 = (3)2 x [(0.36) + (0.64)]
(AC)2 = 9 x 1
(AC) = 3 ----------- equation 1
4) So, the length of the string is 3 m.
5) According to the problem, Nazima pulls in the string at the rate of 5 cm per
second, so, for 12 seconds, the fly comes to point D, so the string pulled by Nazima can be calculated using the formula, distance = speed x time, so we have,
distance of the string pulled = speed x time
distance of the string pulled = 5 x 12
distance of the string pulled = 60 cm
distance of the string pulled = 0.6 m
6) According to the figure, we have,
AD = AC - distance of the string pulled
AD = 3.0 - 0.6
AD = 2.4 m
7) In ∆ ABD, by the theorem of Pythagoras, we get,(BD)2 = (AD)2 - (AB)2
(BD)2 = (2.4)2 - (1.8)2
(BD)2 = (3 x 0.8)2 - (3 x 0.6)2
(BD)2 = (3)2 x [(0.8)2 - (0.6)2]
(BD)2 = (3)2 x [(0.64) - (0.36)]
(BD)2 = 9 x (0.28)
(BD) = 3 x √(0.28)
(BD) = 3 x 0.529
(BD) = 1.587
8) The horizontal distance of a fly from Nazima is DE, so
(DE) = (EB) + (BD)
(DE) = (1.2) + (1.587)
(DE) = 2.787
(DE) = 2.79 m
9) So, the horizontal distance of the fly from Nazima after 12 seconds is 2.79 m.
#mathhelp #NCERT #studentsuccess #Triangles #education #learning #students #teachers #math