127-EMI statement makers for all types of loan

PURPOSE/OBJECTIVES

This tool will help users to verify the EMI statement with the bank’s EMI statement. It will allow users to prevent bank fraudulence if any. 

I faced the same type of problem. A huge amount was included in my loan amount after the payments of 6 EMIs by one of the well-known finance companies which could not be noticed by anyone. At the end of the year, my program was not tallying with the statements of the loan finance company. So, I re-checked my software, thinking that the bank may not do such types of mistakes. I modified my software and checked the statement. There was fraudulence in the bank's statement and the same was sorted out at that time and everything became normal as per my software. So, it will be advantageous to everyone who takes a loan from the bank of any finance company. 

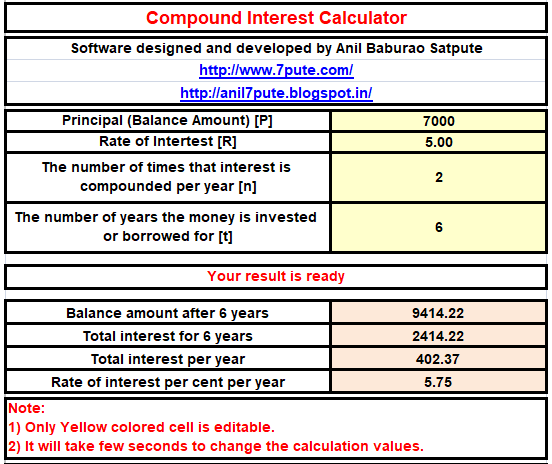
Overview

For any loan taken, we must repay it with equated monthly installments called EMI. This tool requires limited information like: 
1) The opening balance of a loan.
2) EMI-start-Month.
3) EMI amount.
4) Rate of interest.
5) Part payment amounts with month.
6) The details of EMI were skipped.

Based on your information, this tool will calculate the entire EMI account statement, which can be compared with the statement of the loan-providing company.

Procedure

Step-1

Here, enter the principal amount (P), rate of interest (PCPA), (write 13 for 13%), and the number of months of EMI, then we will get the EMI amount. The information will be forwarded for the first-year EMI chart.

The software will take the principal loan amount, rate-of-interest, and EMI starts month directly from the previous sheet. The latest modified information on these fields will be available throughout the EMI charts. 

Step-2

For any changes in the EMI amount, enter the month from the drop-down menu and the new EMI amount in the next cell under the head "EMI".

For any changes in the rate of interest, enter the month from the drop-down menu and the new rate of interest in the next cell under the head "INTEREST".

If any part-payment is done, enter the month from the drop-down menu and the part-payment amount in this cell under the head "Part-Payment".

If any EMI is missed, it will be entered here under the head "EMI not paid for some month".

Step-3

Summary of the EMI statement:

All the information is available in the graph.

ANIL SATPUTE

106-Detailed EMI Statement maker

Purpose/Objectives

The purpose of this tool is to help users to verify their EMI account statement with the bank’s EMI account statement. This tool can help users to prevent bank fraudulence if any. Features like the variable rate of interest, part payment made, and skip of any EMI allow the users to analyze their loan easily.

Overview

For any loan taken, we must repay it with equated monthly installments called EMI. This tool requires limited information like the opening balance of a loan, rate of interest, EMI amount, part payment amounts if any and the details of EMI skipped if any as input. Based on the information this tool will give the entire EMI account statement like the Opening balance of a loan, its interest, the principal amount reduced due to EMI, part payment made, and the closing balance for that respective month.

An educational loan of amount 3394016 is taken at an interest of 13 % pa with an EMI of 55747. EMI started in Oct-2016. Part-payment of 125000 is made in Oct-2016. Then the splitting of EMI 55747 on a loan amount 3394016 at the rate of interest of 13 % per annum for Oct-2016 is 36769 (interest) and 18978 (principal amount). Here the principal amount is reduced by 143978 (125000+18978), so the new closing balance for Oct-2016 is 3250038. See the following diagram.

In Dec-2016 and Feb-2017, these two EMIs were not paid, so they are reflected in the statement. EMI of Dec-2016 was paid in May 2017 and is reflected in the month of May 2017. So, the total EMI for the month of May 2017 (55747) and EMI of Dec 2016 (55747) 111494 is reflected in the month of May 2017. An interest in 55747 for 5 months (Dec-16 to May 2017) at 18% interest in EMI skipped with a penalty for 427 is also reflected on this sheet for all such charges for this year.

This tool takes care of all the criteria such as:

1)      Change in EMI.

2)      Change in rate of interest.

3)      Part payment of a loan.

4)      If any EMI is skipped.

5)      The charges and interest for skipped EMI.

This interactive tool for calculating the entire EMI account statement will help all of us to verify it with the loan provider company.

ANIL SATPUTE

103-Compound interest calculating tool

We will now investigate an issue related to Compound Interest.
Let's explore the concept of Compound Interest with a concrete example.
The following section addresses a common issue related to compound interest.
Now, we will focus on the computation of Compound Interest.
We will examine a typical problem that illustrates the application of Compound Interest.

Compound Interest Calculator

Formula:

A = total amount, P = the principal or the sum of money that is either deposited or borrowed, r = the annual interest rate expressed in decimal form, n = the number of compounding periods each year, and t = the time measured in years.

Example 1: If you invest Rs 7,000 in an account that offers a 5% annual interest rate compounded every two months, what will be the total amount in the account after 6 years? What will be the total interest accrued over 6 years? According to the compound interest formula, what is the annual interest amount and the effective interest rate, PCPA?

Solution:

Given:

Principal amount P = 7000, interest rate r = 0.05, n = 2 (because interest is computed every two months), and t = 6. In this case, we can utilize a logarithm to perform these calculations. Please follow the subsequent steps closely.

Take a look at the software tool designed to obtain these results systematically. Click on the image below and experiment with the outcomes for your values.

The upcoming blog will explore additional software tools for calculating compound interest.

ANIL SATPUTE

102-Tool to calculate difference between two dates (Age calculator)

Click on the following link:

A tool to get the difference between two dates

We are about to explore a handy tool that helps determine the gap between two dates, expressed in years, months, and days. To get started, let’s assess your current age — it’s precise and interactive!
👉 Click on the image below to begin:

Simply enter the necessary details in the Start Date and End Date fields, ensuring the start date precedes the end date. This tool calculates the duration between two dates in years, months, and days.

Whether you're interested in your current age, the age you were when you graduated, or the age gap between you and a relative, this calculator delivers quick and precise results. It's a straightforward yet effective tool for various practical scenarios.

 ANIL SATPUTE

95-Magic Square-14 (Different view)

Click here for the previous part of the magic square.

For centuries, magic squares have intrigued many minds, and now you can delve into their charm with just a simple input—a date!

With our specially crafted software, you can produce 8 varied magic squares, all centered around the date you provide. What sets this tool apart is that in each of the 8 magic squares, the first row will precisely align with the date you entered (formatted as DD-MM-YYYY).

🔍 What occurs next?

After you input a date:

The software swiftly computes and showcases 8 unique magic square designs.

Every square upholds the mathematical balance of a magic square, where the total of every row, column, and diagonal remains constant.

It’s a fascinating mix of mathematical reasoning and imaginative number play, all beginning with a significant date—be it your birthday, anniversary, or another memorable occasion!

🎯 Why give this a try?

It is an entertaining way to witness math in action.

Ideal for students, educators, and inquisitive individuals

Can be utilized in classrooms or simply for enjoyment

👉 Are you ready to witness the enchantment of numbers?

Click the button below to embark on your journey with a date!

Step-1

🧮📲 Tap the link above to begin your journey. After doing so, you'll be directed to a different page where the real excitement unfolds!

Step-2

🟡 Input any date in the yellow cells using the format “DD MM YY YY” (24 04 20 25).

✨ In just a few moments, the first row of all 8 magic squares will be automatically populated with the date you entered. Simultaneously, the other cells will be filled in, allowing you to quickly view eight distinct and intriguing magic squares, each possessing its unique design!

Step-3

🔗 Refer to the illustration below — on the shown page, there’s a link labeled “Click Here to access all addition patterns.”

You will uncover the concealed mathematical symmetries and addition patterns integrated within each magic square by clicking this link.

When you select this link, a new page will appear, showing all the various kinds of addition patterns present in the magic squares.

Understanding the Arrangement of Magic Square Patterns: A Visual Guide

On this newly unveiled page, you will find a unique and organized layout of eight distinct magic squares. The upper section showcases the first four magic squares, while the lower section presents the last four in a visually appealing manner.

To assist you in visualizing and comprehending the concealed symmetries and numerical relationships, elements from both the upper and lower sections are arranged vertically, one below the other, within specially designed tables. This configuration uncovers various types of addition patterns—from Pattern 11 to Pattern 19.

Each table is a showcase of numerical alignments, including the familiar vertical, horizontal, and diagonal, as well as some innovative combinations that will pique your interest. The diagrams, with their highlighted areas, act as visual aids, showing you exactly where these magic squares are and how their elements contribute to each pattern.

📌 For enhanced clarity, please refer to the illustration provided below.

The Entered Portion Will Appear as Follows:

Once you input the date in the specified yellow cells (in the format DD MM YY YY), the upper section of the page—referred to as the entered portion—will display this date as the first row across all 8 magic squares. This visually confirms that the system has accepted your input correctly.

Here is an example of how this entered portion will look on your screen:

This first row serves as the base for each of the 8 distinct magic squares, which are then automatically populated with numbers that preserve the unique magic square properties and addition patterns.

Special thanks to Abhishek Satpute, Aaswad Satpute, and Jyoti Satpute.

ANIL SATPUTE

93-Software to calculate Degree and Radians

a) Click here for "01-Degree-2-Degree-Minute-Second-n-Radian-converter"

b) Click here for "02-Degree-Minute-Second-2-Degree-n-Radian-converter"

c) Click here for "03-Radian-2-Degree-n-Degree-Minute-Second-converter"

1) Directed Angles:

The initial arm rotates through a certain amount of rotation in the clockwise or anti-clockwise direction to the terminal arm then this amount of rotation is called the measure of the directed angle and such an angle is called the directed angle.

The directed angle AOB has ray OA as an initial arm and ray OB as the terminal arm. O is called a vertex of an angle AOB. 

Note: 

1) Here, Angle AOB ≠ Angle BOA even if they have the same amount of rotation.

2) If the rotation of the initial arm is anticlockwise, the directed angle is positive and if it is clockwise then the angle is negative.

See the figure carefully to understand the concept.

91-Magic Square-12 (Software (5 x 5) part-3)

Click here for the previous part of the magic square.

This is the third part of the 5x5 magic square software.

You can enter any 5 numbers between -9999 to 9999 (actually you can enter any number, but for the betterment of the look of the sheet, this restriction is implemented in the software) of your choice in the first row. The software will give you two different magic squares with your chosen numbers in 1 st row. These two magic squares have 120 types of the same addition.

Now the software is uploaded and ready to use.

Rows	5
Columns	5
Diagonals	2
Broken Diagonals	8
Different Patterns	100
Total	120

Click the following button for the software of magic squares of order 5 x 5.

Now we will see all the properties of 5 x 5 magic squares one by one. Let us see the magic squares in which we choose the first row with the numbers 9, 21, 34, 45, and 56. The following two magic squares will be obtained by the software. 

90-Magic Square-11 (Software (5 x 5) part-2)

Click here for the previous part of the magic square.

Prepare your own two magic squares of 5 rows and 5 columns, in which the first row is of your choice. You can enter any 5 numbers between -9999 and 9999 (actually, you can enter any number, but for the betterment of the look of the sheet, this restriction is implemented in the software) of your choice in the first row. The software will give you two different magic squares with your chosen numbers in 1 first row. These two magic squares have 120 types of the same addition.

Rows	5
Columns	5
Diagonals	2
Broken Diagonals	8
Different Patterns	100
Total	120

Click the following button for the software of the magic squares of order 5 x 5.

Now we will see all the properties of 5 x 5 magic squares one by one. Let us examine the magic squares in which we choose the first row to contain the numbers 9, 21, 34, 45, and 56. The following two magic squares will be obtained by the software. 

4) Addition of all the numbers in the Broken Diagonals: (13 to 20)

     a) First Broken Diagonal: (13/20)

09 + 33 + 54 + 23 + 46 = 165         09 + 18 + 38 + 46 + 54 = 165

     b) Second Broken Diagonal: (14/20)

44 + 21 + 52 + 36 + 12 = 165         36 + 21 + 12 + 52 + 44 = 165

     c) Third Broken Diagonal: (15/20)

24 + 55 + 34 + 10 + 42 = 165         55 + 47 + 34 + 19 + 10 = 165

     d) Fourth Broken Diagonal: (16/20)

53 + 32 + 13 + 45 + 22 = 165         22 + 08 + 53 + 45 + 37 = 165

     e) Fifth Broken Diagonal: (17/20)

56 + 44 + 32 + 23 + 10 = 165         56 + 36 + 08 + 46 + 19 = 165

     f) Sixth Broken Diagonal: (18/20)

45 + 33 + 24 + 11 + 52 = 165         45 + 18 + 55 + 35 + 12 = 165

     g) Seventh Broken Diagonal: (19/20)

34 + 20 + 12 + 53 + 46 = 165         34 + 11 + 44 + 22 + 54 = 165

     h) Eighth Broken Diagonal: (20/20)

21 + 13 + 54 + 42 + 35 = 165         21 + 53 + 38 + 10 + 43 = 165

The remaining 100 types of addition patterns will be published in the next blog.

Click here for the next part of the magic square.

ANIL SATPUTE

89-Magic Square-10 (Software (5 x 5) part-1)

Click here for the previous part of the magic square.

Prepare your own two magic squares of 5 rows and 5 columns in which the first row is of your choice. You can enter any 5 numbers between -9999 to 9999 (actually you can enter any number, but for the betterment of the look of the sheet, this restriction is implemented in the software) of your choice in the first row. The software will give you two different magic squares with your chosen numbers in 1 st row. These two magic squares have 120 types of the same addition.

Rows	5
Columns	5
Diagonals	2
Broken Diagonals	8
Different Patterns	100
Total	120

Click the following button for the software of magic squares of order 5 x 5.

Now we will see all the properties of 5 x 5 magic squares one by one. Let us see the magic squares in which we choose the first row with the numbers 9, 21, 34, 45, and 56. The following two magic squares will be obtained by the software. 

Now we will see all types of addition:

1) Addition of all the numbers in the Rows: (1 to 5)

     a) First Row: (1/5)

09 + 21 + 34 + 45 + 56 = 165         09 + 21 + 34 + 45 + 56 = 165

     b) Second Row: (2/5)

44 + 55 + 13 + 20 + 33 = 165         36 + 47 + 53 + 11 + 18 = 165

     c) Third Row: (3/5)

24+ 32 + 43 + 54 + 54 = 165         55 + 47 + 20 + 38 + 44 = 165

     d) Forth Row: (4/5)

55+ 11 + 23 + 36 + 42 = 165         22 + 35 + 46 + 52 + 10 = 165

    e) Fifth Row: (5/5)

35+ 46 + 52 + 10 + 22 = 165         43 + 54 + 12 + 19 + 37 = 165

2) Addition of all the numbers in the Columns: (6 to 10)

     a) First Column: (6/10)

09+ 44 + 24 + 53 + 35 = 165         09 + 36 + 55 + 22 + 43 = 165

     b) Second Column: (7/10)

21+ 55 + 32 + 11 + 46 = 165         21 + 47 + 08 + 35 + 54 = 165

     c) Third Column: (8/10)

34+ 13 + 43 + 23 + 52 = 165         34 + 53 + 20 + 46 + 12 = 165

     d) Forth Column: (9/10)

45 + 20 + 54 + 36 + 10 = 165         45 + 11 + 38 + 52 + 19 = 165

     e) Fifth Column: (10/10)

56 + 33 + 12 + 42 + 22 = 165         56 + 18 + 44 + 10 + 37 = 165

3) Addition of all the numbers in the Diagonals: (11 to 12)

     a) First Diagonal: (11/12)

09 + 55 + 43 + 36 + 22 = 165         09 + 47 + 20 + 52 + 37 = 165

     b) Second Diagonal: (12/12)

56 + 20 + 43 + 11 + 35 = 165         56 + 11 + 20 + 35 + 43 = 165

8 types of broken diagonal addition and 100 types of different patterns of addition will be published in the next blog.

Click here for the next part of the magic square.

ANIL SATPUTE