🌟 Starting a Whimsical Adventure with Numbers!
Today, let’s embark on an exhilarating exploration of the captivating realm of numbers. Numbers resemble stars — bright, limitless, and brimming with fascination. Since my early years, I’ve been delighted to engage with them, discover their hidden patterns, and reveal their mysteries.
Throughout the years, this passion has blossomed into a voyage through the Extraordinary World of Numbers. And the most exciting part? I’ve enjoyed bringing inquisitive minds like yours along for the ride.
Together, let’s journey from one mathematical wonder to another, appreciating the beauty, surprise, and inventiveness that numbers contribute to our existence.
Are you prepared? Let’s set off on this adventure! 🚀
🔢 Unveiling Anilian Numbers
Join us in delving into an intriguing new mathematical idea — Anilian Numbers — a distinctive pattern combining curiosity and logic!
📘 Explanation:
An Anilian number is defined as a number where
The difference between the Left Part and the Right Part
It is precisely equal to the Middle Part.
📌 Additionally, it is crucial that:
Left Part > Right Part
1) In 523, the digit "5" represents the left part, while the digit "3" indicates the right part. The middle part, "2," is obtained by subtracting 3 from 5. In summary, the Middle Part equals the Left Part minus the Right Part. Therefore, 523 qualifies as an "Anilian Number."
📌 It is also crucial that
Left Part > Right Part.
3) 18711. Here, 18 - 11 = 7.
4) 47350 does not qualify as an Anilian number, as 47 - 50 results in -3. The left part is not greater than the right part, so it is not considered an Anilian number.
If we select a number and repeatedly add it to itself in a specific arrangement for a certain number of times, we arrive at what is known as an Anilian number.
Example 01:
Let's consider the number 243. As illustrated below, arrange this number in a zigzag format for 14 repetitions and compute the sum. The result will be an Anilian number.
The figure above depicts the configuration of digit 243. These digits are used 14 times total. We then sum these digits together. This sum equals 18711. Since 18 - 11 equals 7, 18711 is identified as an Anilian number. This technique is referred to as anilofication.
Example 02:
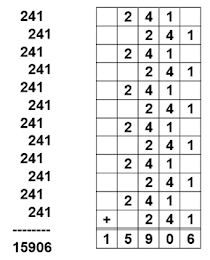
Let's consider the number 241. As illustrated below, organize this number in a zigzag format, repeat the process 12 times, and then sum the results. The final result will be an Anilian number.
Let's consider the number 241. As illustrated below, organize this number in a zigzag format, repeat the process 12 times, and then sum the results. The final result will be an Anilian number.
As illustrated in the figure, we need to organize 241 exactly 12 times. The sum is 15906; since 15 - 06 equals 9, 15906 is classified as an Anilian number.
Example 03:
Let's consider the number 351. As demonstrated below, organize this number in a zigzag pattern for 14 iterations and calculate the sum. The result we obtain is known as an Anilian number.
Example 03:
Let's consider the number 351. As demonstrated below, organize this number in a zigzag pattern for 14 iterations and calculate the sum. The result we obtain is known as an Anilian number.
In this section, we must organize the number 351 exactly 14 times, as illustrated in the diagram. The sum is represented as 27027, and since 27 - 27 equals 0, we conclude that 27027 is an Anilian Number. With the middle number being 0, we refer to this Anilian number as a standard Anilian number.
Happy Work:
1) Please select the number 503 and organize it as shown for 14 repetitions. Verify if the result is an Anilian number.
Happy Work:
1) Please select the number 503 and organize it as shown for 14 repetitions. Verify if the result is an Anilian number.
You can experiment with any number. This is an excellent concept that I developed in my childhood.
Please respond to me at my email address: anil@7pute.com.


No comments:
Post a Comment