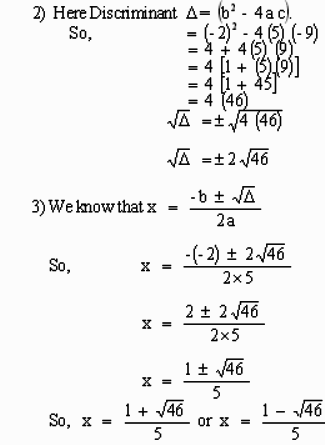65-06 Basics of Quadratic Equations

Click here for the previous basics.

Now we will see a few quadratic equations using the formula method.

a) Solve the quadratic equation  5 x ² - 2 x - 9 = 0.

Solution:

       1) Comparing  5 x ² - 2 x - 9 = 0 with a x ² + b x + c = 0 we get,

            a = 5, b = - 2, c = - 9

b) Solve the quadratic equation  3 x ² - 4 x - 3 = 0.

Solution:

       1) Comparing  3 x ² - 4 x - 3 = 0  with a x ² + b x + c = 0 we get,

            a = 3, b = - 4, c = - 3

Now we will see some rules about the roots of the quadratic equation.

       1) Sum of the roots (α, β) of the quadratic equation a x ² + b x + c = 0,

              α  +  β  =  - b / a  and   α β  =  c / a

              α  +  β  =  - Coefficient of x / Coefficient of x ²  and   α β  =  Constant / Coefficient of x ^2.

       2) If α and β are the roots of the quadratic equation then the quadratic equation will be 

            x ² - (Sum of the roots)  x + (Product of the roots) = 0,

            x ² - (α  +  β)  x + (α β) = 0,

^{Now we will see some important problems in Quadratic equations and the roots of the Quadratic Equations}

       ^{a) If the sum of the roots of the quadratic equation is 3 and the sum of their cubes is 63, then find the equation.}

         ^Solution:

          1)  Here, α + β =  3 and  α ³ + β ³ =  63

          2)  We know that , α ³ + β ³ =  (α + β)³ - 3 α β (α + β)

                                   so ,     63      =  (3)³ - 3 α β (3)

                                               63      =  27 - 9 α β       Dividing by 9 through out we get

                                                7       =  3  - α β 

                                                 α β   =  3  - 7 

                                                 α β   =  - 4

          3) We know that  the quadratic equation will be 

                       x ² - (α  +  β)  x + (α β) = 0 

                       x ² - (3)  x + (- 4) = 0 

                       x ² - 3 x - 4 = 0 

          4)  Answer: So the required quadratic equation will be x ² - 3 x - 4 = 0.

A few more problems on Quadratic Equations related to factors will be discussed in the next Blog.

Click here for the next basics.

Anil Satpute

64-05 Basics of Quadratic Equations

Click here for the previous basics.

c]  Solve the quadratic equation  a x ² + b x + c = 0 using perfect square method.

Solution:

      1) Shift c to RHS we get  a x ² + b x  = - c 

      2) Dividing the equation by " a " throughout 

          So,   x ² + (b / a) x  = - (c / a) 

               Here, third term = ( 1/2 coefficient of  x ) ² 

                                         = ( 1/2 (b / a) ) ²

                                         = (b / 2 a) ²

                                         = b ²/ 4 a ²

Now we will see a few quadratic equations using the formula method.

a) Solve the quadratic equation  x ² - 4 x - 21 = 0.

Solution:

       1) Comparing  x ² - 4 x - 21 = 0 with a x ² + b x + c = 0 we get,

            a = 1, b = - 4, c = - 21

       2) Here Discriminant

                                                =  (- 4 )² - 4 (1) ( - 21) 

                                                =  16 + 84       

                                                =  100

A few more problems on Quadratic Equations related to factors will be discussed in the next Blog.

Click here for the next basics.

Anil Satpute

63-04 Basics of Quadratic Equations

Click here for the previous basics.

Now we will see the important problems of quadratic equations to be solved using the perfect square method:

Few steps to be followed to solve the quadratic equation using the perfect square method:
              1) Shift the constant term to the right-hand side of the equation.

              2) Divide both sides of the equation by the coefficient of x ². 
              3) Find the third term of the left-hand side to make it a perfect square.
              4) Use the formula " Third Term = ( 1/2 coefficient of x ) ². 
              5) Add this third term so obtained as mentioned in step 4 on both sides of the equation.

Please REMEMBER the above 5 steps to get your answer quickly and without any mistakes. 
a]  Solve the quadratic equation  x ² - 18 x  + 65 = 0 using perfect square method.

Solution:

      1) Shift 65 to RHS

      2)  x ² - 18 x  = - 65                  Here third term = ( 1/2 coefficient of  x ) ² 

                                                                                = ( 1/2 (18) ) ²

                                                                                = ( 9 ) ²

                                                                                = 81

           x ² - 18 x  + 81 = - 65 + 81

                   ( x  - 9 ) ² = 16

                     ( x  - 9 )  = + 4 or ( x  - 9 )  = - 4 

                                x  = 9 + 4 or  x  =  9 - 4 

                                x  = 13 or  x  =  5

        3)  So the roots of the equation are 5 or 13 so Solution Set = { 5, 13 }  

b]  Solve the quadratic equation  x ² - 5 x  + 6 = 0 using perfect square method.

Solution:

      1) Shift 6 to RHS

      2)  x ² - 5 x  = - 6                  Here third term = ( 1/2 coefficient of  x ) ² 

                                                                                = ( 1/2 (5) ) ²

                                                                                = ( 5/2 ) ²

                                                                                = 25/4

           x ² - 5 x  + 25/4 = - 6 + 25/4

                   ( x  - 5/2 ) ² = (25-24)/4

                   ( x  - 5/2 ) ² = 1/4

                     ( x  - 5/2 )  = + 1/2 or ( x  - 5/2 )  = - 1/2 

                                x  = 5/2 + 1/2 or  x  =  5/2 - 1/2 

                                x  = 6/2 or  x  =  4/2

                                x  = 3 or  x  =  2

        3)  So the roots of the equation are 2 or 3 so Solution Set = { 2, 3 }  

c]  Solve the quadratic equation  x ² - 6 x  + 2 = 0 using perfect square method.

Solution:

      1) Shift 2 to RHS

      2)  x ² - 6 x  = - 2                  Here third term = ( 1/2 coefficient of  x ) ² 

                                                                                = ( 1/2 (- 6) ) ²

                                                                                = ( - 3 ) ²

                                                                                = 9

           x ² - 6 x  + 9 = - 2 + 9

                   ( x  - 3 ) ² =  7

                     ( x  - 3 )  = + √ 7 or ( x  - 3 )  = - √ 7 

                                x  = 3 + √ 7 or  x  =  3 - √ 7

                                x  = 3 + √ 7 or  x  =  3 - √ 7

        3)  So the roots of the equation are 3 + √ 7 or 3 - √ 7 so Solution Set = { 3 + √ 7,  3 - √ 7 }  

d]  Solve the quadratic equation  x ² - 5 x  + 2 = 0 using perfect square method.

Solution:

    1) Shift 2 to RHS

    2)  x ² - 5 x  = - 2                  Here third term = ( 1/2 coefficient of  x ) ² 

                                                                                = ( 1/2 (- 5) ) ²

                                                                                = ( - 5/2 ) ²

                                                                                = 25/4

           x ² - 5 x  + 25/4 = - 2 + 25/4

                   ( x  - 5/2 ) ² =  (- 8 + 25)/4

                   ( x  - 5/2 ) ² =  17/4

                     ( x  - 5/2 )  = + (√ 17)/2 or ( x  - 5/2 )  = -  (√ 17)/2 

                                x  = 5/2 + (√ 17)/2 or  x  =  5/2 - (√17)/2

                                x  = (5 + √ 17)/2 or  x  =  (5 - √ 17)/2

     3)  So the roots are (5 + √ 17)/2 or (5 - √ 17)/2 so Solution Set = {(5 + √ 17)/2,  (5 + √ 17)/2 }  

Please write your opinions about the methods given for these problems. My email id is: anil@7pute.com

A few more problems on Quadratic Equations will be discussed in the next Blog.

Click here for the next basics.

Anil Satpute

62-03 Basics of Quadratic Equations

Click here for the previous basics.

Some special and critical types of factors:

Please download the following file and study it very carefully so that you will not find any difficulties while solving quadratic equations. Download the following file by clicking on it.

Click here to download the critical-type-of-factors.pdf file.

Just go through this downloaded file and be prepared to solve any problem pertaining to these critical factors.

Now we will see a few more important problems of quadratic equations:

d]  Solve the quadratic equation  x ² - 18 x  + 65 = 0 using factorization method.

Solution:

      1) The coefficient of x ²  is 1 and the sign of the constant term  65 is " + ".

      2)  So,           x ² - 18 x  + 65 = 0                  Here the factors of 1 & 65 are 
                                                                                5 x 13
                                                                                as we want the sum as 18
                                                                                so we have to take 5 & 13
                                                                                5 x 13
                             x ² - 5 x - 13 x  + 65 = 0
                       x ( x  -  5 )  -  13 ( x  -  5 ) = 0
                        ( x  -  5 )  ( x  -  13 ) = 0
                        ( x  -  5 )  =  0  or  ( x  -  13 ) = 0
                         x  =  5  or   x  =  13
                         x  =  5  or  x  =  13
       3)  So the roots of the equation are 5 or 13 so Solution Set = { 5, 13 }  

e]  Solve the quadratic equation  x ² - 24 x  + 143 = 0 using factorization method.

Solution:

      1) The coefficient of x ²  is 1 and the sign of the constant term  143 is " + ".

      2)  So,           x ² - 24 x  + 143 = 0                  Here 143 is odd so 2, 4, 6, and 8 are not the factors of           

                                                                             143. Similarly 1 + 4 + 3 = 8, which is not divisible by 3 

                                                                             & 9 so 3 & 9 are also not the factors of 143. The unit digit  

                                                                             is not 5 or 0 so 5 and 10 are not the factors of 143. 

                                                                             Sum of digit at unit place & 100th place is 1 + 3 = 4  

                                                                             which is the same as the digit in 10th place so 11 is the  

                                                                             the factor of 143  so here factors 1 & 143 will be 

                                                                             11 x 13
                             x ² - 11 x - 13 x  + 143 = 0
                       x ( x  -  11 )  -  13 ( x  -  11 ) = 0
                        ( x  -  11 )  ( x  -  13 ) = 0
                        ( x  -  11 )  =  0  or  ( x  -  13 ) = 0
                         x  =  11  or   x  =  13
                         x  =  5  or  x  =  13
       3)  So the roots of the equation are 11 or 13 so Solution Set = { 11, 13 }  

f]  Solve the quadratic equation  5 x ² + 56 x  + 11 = 0 using factorization method.

Solution:

      1) The coefficient of x ²  is 5 and the sign of the constant term  11 is " + ".

      2)  So,          5 x ² + 56 x  + 11 = 0                  Here the factors of 5 & 11 with addition as 56 are 
                                                                             55 x 1
                                                                             as we want the sum as 56
                                                                             so we have to take 55 & 1
                                                                             55 x 13
                          5  x ² + 55 x  +  x  + 11 = 0
                     5 x ( x  +  11 )  +  ( x  +  11 ) = 0
                        ( 5 x  +  1 )  ( x  +  11 ) = 0
                        ( 5 x  +  1 )  =  0  or  ( x  +  11 ) = 0
                       5 x  =  - 1  or  x  =  - 13
                         x  =  - 1/5  or  x  =  - 11
       3)  So the roots of the equation are - 1/5 or - 11 so Solution Set = { - 1/5, - 11 }  

g]  Solve the quadratic equation  2 x ² + 21 x  + 45 = 0 using factorization method.

Solution:

      1) The coefficient of x ²  is 2 and the sign of the constant term  45 is " + ".

      2)  So,          2 x ² + 21 x  + 45 = 0                  Here the factors of 2 & 45 with addition as 21 are 
                                                                             2 x 45

                                                                             2 x 5 x 9

                                                                             2 x 5 x 3 x 3

                                                                             (2 x 3) x (5 x 3)

                                                                             6 x 15
                                                                             as we want the sum as 21
                                                                             so we have to take 6 & 15
                                                                             6 x 15
                          2 x ² + 6 x  + 15 x + 45 = 0 
                     2 x ( x  +  3 )  + 15 ( x  +  3 ) = 0
                        ( 2 x  +  15 )  ( x  +  3 ) = 0
                        ( 2 x  +  15 )  =  0  or  ( x  +  3 ) = 0
                       2 x  =  - 15  or  x  =  - 3
                         x  =  - 15/2  or  x  =  - 3
       3)  So the roots of the equation are - 15/2 or - 3 so Solution Set = { - 3, - 15/2 }  

h]  Solve the quadratic equation   x ² + 5 √3 x  + 18 = 0 using factorization method.

Solution:

      1) The coefficient of x ²  is 1 and the sign of the constant term  18 is " + ".

      2)  So,          x ² + 5 √3 x  + 18 = 0                  Here the factors of 1 & 18 with addition as 5 √3 are 
                                                                             1 x 18

                                                                             3 x 2 x 3

                                                                             (2 √3) x (3 √3)

                                                                             as we want the sum as 5 √3
                                                                             so we have to take 2 √3 & 3 √3
                                                                             6 x 15
                           x ² + 2 √3 x  + 3 √3 x + 18 = 0 

                       x ( x  +  2 √3 )  + 3 √3 ( x  +  2 √3 ) = 0

                        ( x  +  2 √3 )  ( x  +  3 √3 ) = 0
                        ( x  +  2 √3 )  =  0  or  ( x  +  3 √3 ) = 0
                        x  =  - 2 √3  or  x  =  - 3 √3
       3)  So the roots of the equation are - 2 √3 or - 3 √3 so Solution Set = { - 2 √3  - 3 √3 }  

A few more problems on Quadratic Equations related to factors will be discussed in the next Blog.

Click here for the next basics.

Please write your opinions about the methods given for these problems.

Anil Satpute