NCERT
10th Mathematics
Exercise 10.1
Topic: Circle
We're here to help! If you're looking for resources to help you learn math, you've come to the right place. We have NCERT textbooks, lessons on Circle, and more. Join our community of students and teachers today!
1. How many tangents can a circle have?
Ans:
A circle can have infinite tangents due to its unique
properties.
1. How many tangents can a circle have?
Ans:
A circle can have infinite tangents due to its unique
properties.
1) From Points Outside the Circle: There are infinitely many pairs of tangents for each point outside the circle, as there are exactly two tangents drawn to the circle for each point.
2) From Points on the Circle: The circumference of a circle can be drawn from every point, resulting in infinitely many tangents, as there are infinitely many points on the circle's circumference.
2. Fill in the blanks :
(i) A tangent to a circle intersects it in ____________ point (s).
(ii) A line intersecting a circle in two points is called a ___________.
(iii) A circle can have ____________ parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called _____________.
Ans:
(i) A tangent to a circle intersects it in one point (s).(ii) A line intersecting a circle in two points is called a secant.(iii) A circle can have two parallel tangents at the most.(iv) The common point of a tangent to a circle and the circle is called the point
of contact.
3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the
center O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119 cm.
Solution:
1) PQ is the tangent to the circle with center O at point P.
2) OP = 5 cm is the radius, and OQ = 12 cm.
3) In ∆ OPQ, by the theorem of Pythagoras, we get,
(PQ)2 + (OP)2 = (OQ)2
(PQ)2 = (OQ)2 – (OP)2
(PQ)2 = (12)2 – (5)2
(PQ)2 = 144 – 25
(PQ)2 = 119
PQ = √119
4) PQ = √119 cm.
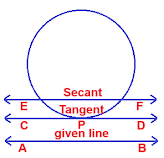
4. Draw a circle and two lines parallel to a given line such that one is a
tangent and the other, a secant to the circle.
Solution:
#mathhelp #NCERT #studentsuccess #Circle #education #learning #students #teachers #math
No comments:
Post a Comment